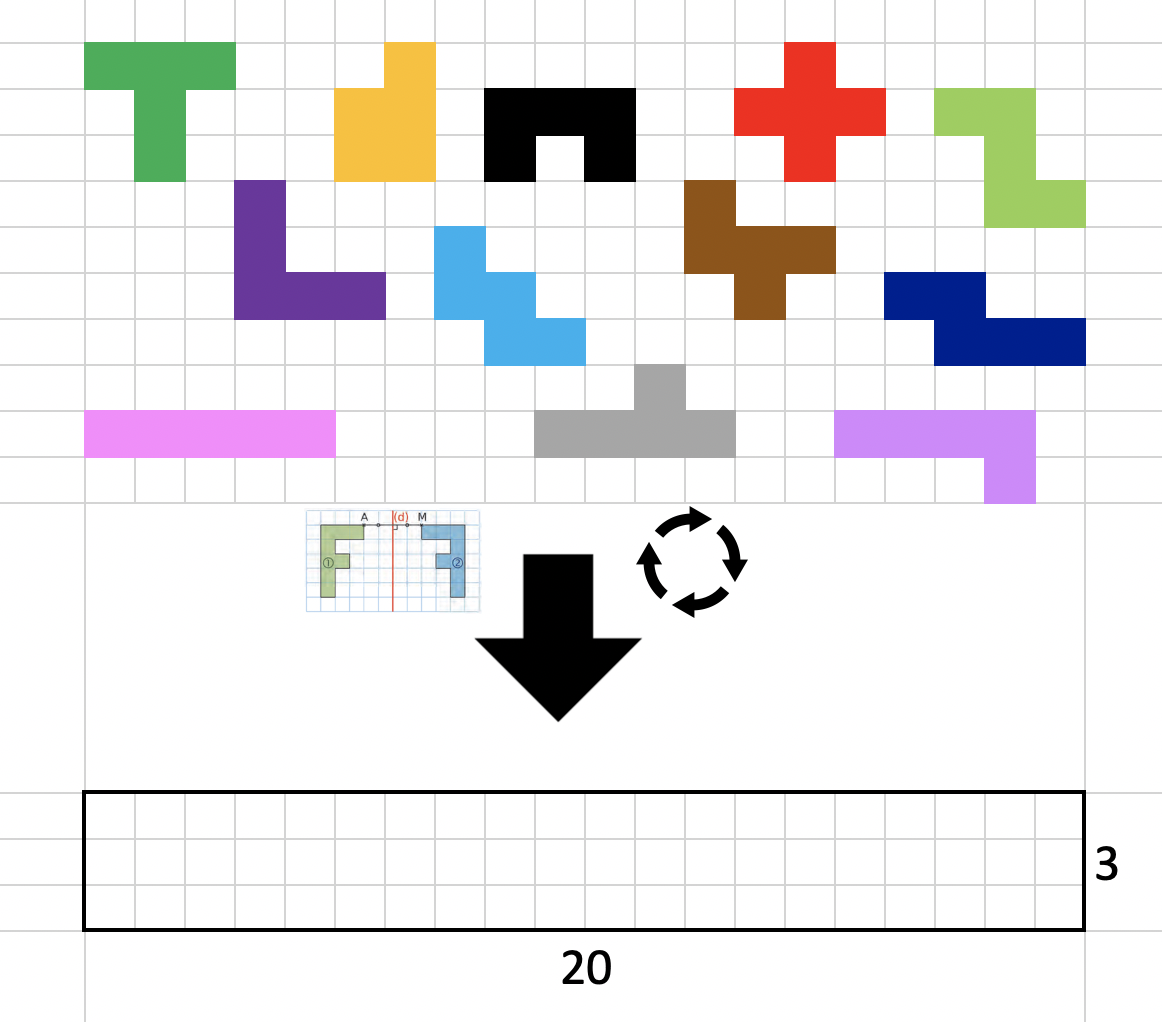
Pentominos
Énigme issue du chapitre 74 du magnifique livre d'énigme "Les Énigmes de Canterbury" du mathématicien génial Henry E. Dudeney et dont on en trouve rapide exposition sur wikipédia : https://fr.wikipedia.org/wiki/Pentomino.
il s'agit de
1 Former tous les arrangements connexes possibles de cinq carrés à la rotation et à la symétrie près. (il y en 12)
2 Disposer les douze pentominos (5x12) obtenus sur un rectangle de 3x20
https://github.com/linol/python/tree/master/pentominos
Dans un premier temps on va bien modéliser chacun des acteurs qui sont en jeu.
Ensuite on s'emploiera à placer des pentominos sur la surface à remplir en vérifiant quand cela est possible.
Puis on cherchera des méthodes simples de résolution
Enfin on trouvera des moyens d'optimiser les calculs.
Mais avant toute chose prenons le temps de bien définir les termes de notre problème
Quelques définitions
Pentominos : Un pentomino ou pentamino est une figure géométrique constituée de 5 carrés accolés par un de leurs côtés, c'est un cas particulier de polyomino.(cf : https://fr.wikipedia.org/wiki/Pentomino). Les pentominos que l'on utilisera sont classés à la rotation et à la symétrie près.
Agencement : Déclinaisons d'un pentominos à la rotation et à la symétrie près
Map : On appellera "map" la surface à remplir par les pentominos (ici un rectangle de 3x20)
Case vide: Une case vide est un emplacement de la map qui contient exactement 0
Cases voisines : On désignera par cases voisines d'une case les cases situées directement dessus, dessous, à gauche et à droite.
Composante : On appellera "composante" un groupe de cases vides voisines de la map
L'algorithme se trouve dans le fichier
https://github.com/linol/python/blob/master/pentominos/pentominos.py
qui utilise les fonctions du fichier https://github.com/linol/python/blob/master/pentominos/pentominos_functions.py
dont les fonctions principales font objets de tests détaillés dans le fichier
https://github.com/linol/python/blob/master/pentominos/pentominos_unittests.py
La map
Nous modéliserons la surface à remplir par un tableau à deux dimensions d'une taille de 3 par 20 comme ceci :
map = [
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]
Les pentominos
On représentera tous les pentominos par une liste contenant toutes les déclinaisons de chacun d'eux à la rotation et à la symétrie près.
On utilisera la plus petite liste à deux dimensions possible pour les représenter.
Et on utilisera un chiffre ou une lettre pour reconnaître le pentomino un fois posé sur la map.
Exemple :
[
[
[9,9,0],
[0,9,0],
[0,9,9]
],[
[0,0,9],
[9,9,9],
[9,0,0]
],[
[0,9,9],
[0,9,0],
[9,9,0]
],[
[9,0,0],
[9,9,9],
[0,0,9]
]
]
L'ensemble des pentominos est recensé dans le fichier : https://github.com/linol/python/blob/master/pentominos/pentominos_items.py
Placer un pentomino consiste à affecter aux cases de la map les cases non vides du pentomino (à partir d'un endroit situé sur la map).
exemple : plaçons le pentomino suivant "[1, 1, 1, 1, 1] " sur la map vide en haut à gauche (alias map[0][0]) .
On utilise de ce fait la fonction
map = setPentomino(map, 0, 0, pentominos[0][1])
qui prend comme arguments
- "map" : qui est la map que l'on considère,
- 0 , 0 : qui sont les coordonnées de la map à partir desquelles on souhaite placer notre pentomino et
- pentominos[0][1] qui désigne le pentomino ("0") que l'on souhaite placer avec sa déclinaison("1")
Cette fonction renvoie la map avec ledit pentomino placé.
Ainsi le résultat attendu de notre opération est le suivant :
exceptedMap = [
[1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]
Placer des pentominos avec retrait
Ensuite on cherchons à placer le pentomino suivant : [[0, 2, 0], [2, 2, 2], [0, 2, 0]] à partir de la premère case vide que l'on trouve (ici map[0][5]).
Si on applique exactement le même principe que pour le placement du pentomino précédent on devrait obtenir le résultat suivant :
[
[1, 1, 1, 1, 1, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]
Alors que le résultat que nous attendons est celui-là :
exceptedMap = [
[1, 1, 1, 1, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
]
Il est donc nécessaire de décaler le placement du pentomino par le nombre de cases vides qui entre dans sa définition.
D'autre exemples se trouvent dans la fonction 'test_setPentominoAvecRetrait' du cahier de tests: https://github.com/linol/python/blob/master/pentominos/pentominos_unittests.py
Étude de possibilité du placement d'un pentomino
Deux contraintes se posent sur la possiblilté de placer un pentomino
- la dimension de la map
- les cases occupées par d'autres pentominos
Cette étude est faite par la fonction
isPossibleSetPentomino(map, 0, 0, pentominos[0][1])
avec le même description des arguments que pour la fonction "setPentomino" mais qui renvoie un booléen suivant le cas.
Des exemples plus précis se trouvent avec le test "test_isPossibleSetPentomino" du cahier de test.(https://github.com/linol/python/blob/master/pentominos/pentominos_unittests.py)
Remarques:
- Ce calcul de retrait est observé sur le placement et sur la possibilité d'ajouter un pentomino sur la map.
- Même si par la suite on utilisera souvent des fonctions qui contiennent la map, il n'est pas recommandé ici d'utiliser la programmation orientée objet (notamment pour les pasages par valeur et par référence que l'on abordera plus tard)
Une méthode simple consiste à dire que l'on cherche à placer des pentominos sur la map jusqu'à ce que leurs positionnements couvre l'intégralité de la map. ainsi on pourra considérer que l'on a obtenu une solution s'il ne reste plus aucune case vide sur la map.
Comment va-t-on chercher à placer nos pentominos?
On place, si c'est possible , le premier pentomino de la liste à partir de la première case vide disponible.
On retire le pentomino de la liste des pentominos et
on réitère (avec le pentomino placé).
Si le placement n'est pas possible on essaie avec un autre agencement et
si toutefois le placement du pentominos est impossible queque soit son agencement
on essaie avec le pentomino suivant
tant qu'il reste au moins une case vide.
Ainsi on utilisera un algorithme récursif.
Passage par valeur et par référence :
par défaut (contrairement à d'autres langages) python utilise le passage par référence.
Il s'agira donc de travailler sur un copie de la map courrante notamment pour pouvoir revenir en arrière.(qui correspond à l'étape "on passe au pentomino suivant" ou "on essaie avec un autre agencement")
Premier résultat : On croirait être tombé dans une boucle infini !!! le temps de calcul est astronomique (se compte en jours).
J'ai un peu de mal à calculer rigoureusement la complexité de cet algorithme.
Un premier aménagement de notre algorithme va consister à suivre l'évolution de celui-ci notamment en mentionnant les pentominos que l'on a réussit à placer. C'est l'objet de la variable "state".
D'autre part, on va chercher à éliminer des cas impossbiles (même si le placement d'un pentomino est possible).
Éliminer les situtations impossibles
Par exemple :
exempleMap = [
['x','x','x','x','x','x', 0 , 0 , 0 , 0 , 0 ,'x','x','x','x','x','x','x','x','x'],
['x','x', 0 , 0 ,'x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x'],
['x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x','x']
]
Alors le pentomino [[1, 1, 1, 1, 1]] est bien positionnable sur la map. on ne pourra pas trouver de solution puisqu'aucun pentomino ne pourra être placé dans les deux cases vides isolées.
En fait, comme par définition nos pentominos sont tous constitués de 5 cases, on peut même déduire qu'une map contenant au moins un groupe de moins de 5 cases isolées ne pourra être une des solutions que l'on cherche.
Ainsi on définira par "composante" un ensemble de cases vides voisines au sein de la map.
Il s'agit alors de trouver toutes les composantes que l'on peut observer au sein d'une map.
C'est le calcul qui est fait par la fonction
getComposantes(map)
Trouver une componsante consiste à
à partir d'une case vide,
relever les cordonnées de cette case,
retirer cette case des cases vides que l'on cherche (c'est à dire que l'on remplira la case avec une valeur arbitraire)
puis réitérer sur toutes les cases vides voisines.
Et donc trouver toutes les composantes de notre map consiste à trouver une composante tant que l'on trouve des cases vides sur la map.
Ici contrairement à l'algorithme précédent, il est important de considérer toujours la même map tant que le calcul des composantes n'est pas fini.
Cette vérification est à faire aussitôt après avoir placé un pentomino et à inclure dans la fonction "isPossibleSetPentomino"
Commencer par les cas les plus contraignants
Issue du même principe, on peut en déduire une méthode plus performante à qui consitera à chercher à placer les pentominos restants au sein de la plus petite des composantes que l'on sait maintenant calculer.
Issue de ce calcul, on obtient toutes les solutions possibles dans un temps plus ou moins raisonnable. C'est à dire un peu plus de 7 heures. Le recensement des résultats se fait en affichant la map dès qu'il n'y a plus de case vide.
Evidemment certaines solutions sont symétriques. on relèvera deux familles de solutions composés de :
4 4 2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c a
4 2 2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c a
4 4 2 3 3 3 9 7 7 7 7 6 5 8 b b b a a a
4 4 2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9 a
4 2 2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9 a
4 4 2 3 3 3 c c c c 8 5 5 5 6 6 9 a a a
Et ci-desous l'intégralité des solutions trouvées.
Certaines solutions, qui ont été trouvées par la prise en compte du retrait de positionnement, sont à exclures :
2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c a 4 4
2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c a 4 2
2 3 3 3 9 7 7 7 7 6 5 8 b b b a a a 4 4
2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9 a 4 4
2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9 a 4 2
2 3 3 3 c c c c 8 5 5 5 6 6 9 a a a 4 4
2 3 3 3 9 7 7 7 7 6 5 8 b b b a a a 4 4
2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c a 4 2
2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c a 4 4
2 3 3 3 c c c c 8 5 5 5 6 6 9 a a a 4 4
2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9 a 4 2
2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9 a 4 4
2 4 4 a 9 7 7 7 7 6 5 8 b b b 1 1 1 1 1
2 2 4 a 9 9 9 7 6 6 5 8 8 8 b b c 3 3 2
2 4 4 a a a 9 6 6 5 5 5 8 c c c c 3 3 3
2 4 4 a c c c c 8 5 5 5 6 6 9 1 1 1 1 1
2 2 4 a c b b 8 8 8 5 6 6 7 9 9 9 3 3 2
2 4 4 a a a b b b 8 5 6 7 7 7 7 9 3 3 3
2 4 4 a a a 9 6 6 5 5 5 8 c c c c 3 3 3
2 2 4 a 9 9 9 7 6 6 5 8 8 8 b b c 3 3 2
2 4 4 a 9 7 7 7 7 6 5 8 b b b 1 1 1 1 1
2 4 4 a a a b b b 8 5 6 7 7 7 7 9 3 3 3
2 2 4 a c b b 8 8 8 5 6 6 7 9 9 9 3 3 2
2 4 4 a c c c c 8 5 5 5 6 6 9 1 1 1 1 1
4 4 2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c a
4 2 2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c a
4 4 2 3 3 3 9 7 7 7 7 6 5 8 b b b a a a
4 4 2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9 a
4 2 2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9 a
4 4 2 3 3 3 c c c c 8 5 5 5 6 6 9 a a a
4 4 2 3 3 3 9 7 7 7 7 6 5 8 b b b a a a
4 2 2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c a
4 4 2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c a
4 4 2 3 3 3 c c c c 8 5 5 5 6 6 9 a a a
4 2 2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9 a
4 4 2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9 a
5 6 7 7 7 7 9 3 3 3 2 4 4 a a a b b b 8
5 6 6 7 9 9 9 3 3 2 2 2 4 a c b b 8 8 8
5 5 6 6 9 1 1 1 1 1 2 4 4 a c c c c 8 5
5 6 7 7 7 7 9 a 4 4 2 1 1 1 1 1 b b b 8
5 6 6 7 9 9 9 a 4 2 2 2 3 3 c b b 8 8 8
5 5 6 6 9 a a a 4 4 2 3 3 3 c c c c 8 5
5 8 b b b 1 1 1 1 1 2 4 4 a 9 7 7 7 7 6
5 8 8 8 b b c 3 3 2 2 2 4 a 9 9 9 7 6 6
5 5 8 c c c c 3 3 3 2 4 4 a a a 9 6 6 5
5 8 b b b a a a 4 4 2 3 3 3 9 7 7 7 7 6
5 8 8 8 b b c a 4 2 2 2 3 3 9 9 9 7 6 6
5 5 8 c c c c a 4 4 2 1 1 1 1 1 9 6 6 5
6 5 8 b b b 1 1 1 1 1 2 4 4 a 9 7 7 7 7
6 5 8 8 8 b b c 3 3 2 2 2 4 a 9 9 9 7 6
5 5 5 8 c c c c 3 3 3 2 4 4 a a a 9 6 6
6 5 8 b b b a a a 4 4 2 3 3 3 9 7 7 7 7
6 5 8 8 8 b b c a 4 2 2 2 3 3 9 9 9 7 6
5 5 5 8 c c c c a 4 4 2 1 1 1 1 1 9 6 6
6 6 9 1 1 1 1 1 2 4 4 a c c c c 8 5 5 5
6 7 9 9 9 3 3 2 2 2 4 a c b b 8 8 8 5 6
7 7 7 7 9 3 3 3 2 4 4 a a a b b b 8 5 6
6 6 9 a a a 4 4 2 3 3 3 c c c c 8 5 5 5
6 7 9 9 9 a 4 2 2 2 3 3 c b b 8 8 8 5 6
7 7 7 7 9 a 4 4 2 1 1 1 1 1 b b b 8 5 6
8 5 6 7 7 7 7 9 3 3 3 2 4 4 a a a b b b
8 5 6 6 7 9 9 9 3 3 2 2 2 4 a c b b 8 8
5 5 5 6 6 9 1 1 1 1 1 2 4 4 a c c c c 8
8 5 6 7 7 7 7 9 a 4 4 2 1 1 1 1 1 b b b
8 5 6 6 7 9 9 9 a 4 2 2 2 3 3 c b b 8 8
5 5 5 6 6 9 a a a 4 4 2 3 3 3 c c c c 8
8 c c c c 3 3 3 2 4 4 a a a 9 6 6 5 5 5
8 8 b b c 3 3 2 2 2 4 a 9 9 9 7 6 6 5 8
b b b 1 1 1 1 1 2 4 4 a 9 7 7 7 7 6 5 8
8 c c c c a 4 4 2 1 1 1 1 1 9 6 6 5 5 5
8 8 b b c a 4 2 2 2 3 3 9 9 9 7 6 6 5 8
b b b a a a 4 4 2 3 3 3 9 7 7 7 7 6 5 8
a 9 7 7 7 7 6 5 8 b b b 1 1 1 1 1 2 4 4
a 9 9 9 7 6 6 5 8 8 8 b b c 3 3 2 2 2 4
a a a 9 6 6 5 5 5 8 c c c c 3 3 3 2 4 4
a c c c c 8 5 5 5 6 6 9 1 1 1 1 1 2 4 4
a c b b 8 8 8 5 6 6 7 9 9 9 3 3 2 2 2 4
a a a b b b 8 5 6 7 7 7 7 9 3 3 3 2 4 4
a a a 9 6 6 5 5 5 8 c c c c 3 3 3 2 4 4
a 9 9 9 7 6 6 5 8 8 8 b b c 3 3 2 2 2 4
a 9 7 7 7 7 6 5 8 b b b 1 1 1 1 1 2 4 4
a a a b b b 8 5 6 7 7 7 7 9 3 3 3 2 4 4
a c b b 8 8 8 5 6 6 7 9 9 9 3 3 2 2 2 4
a c c c c 8 5 5 5 6 6 9 1 1 1 1 1 2 4 4
a 4 4 2 1 1 1 1 1 9 6 6 5 5 5 8 c c c c
a 4 2 2 2 3 3 9 9 9 7 6 6 5 8 8 8 b b c
a 4 4 2 3 3 3 9 7 7 7 7 6 5 8 b b b a a
a 4 4 2 1 1 1 1 1 b b b 8 5 6 7 7 7 7 9
a 4 2 2 2 3 3 c b b 8 8 8 5 6 6 7 9 9 9
a 4 4 2 3 3 3 c c c c 8 5 5 5 6 6 9 a a
On peut sans doute trouver d'autres critères ou d'autres méthodes afin de trouver des solutions plus rapidement.
En peut aussi fractionner (et paralléliser) le calcul en forçant l'algorithme à commencer par l'agencement d'un pentomino en particulier.
Il serait sans doute intéressant de voir comment pourrait fonctionner une IA sur ce genre de problème.
On peut chercher aussi à remplir d'autres formes de map, à partir du moment où celles-ci contiennent bien 60 cases (évidemment) et on peut chercher aussi des solutions sur des figures à trois dimensions (exemple 3x4x5).

